Periodo de Retorno

Es un hecho probado, contrastado, demostrado y reiterado que una secuencia de datos debidamente “torturada” puede utilizarse para justificar cualquier cosa, especialmente en manos políticas. Entre las herramientas de tortura numérica más eficientes destaca la estadística, a menudo ayudada de gráficos engañosos, pero incluso dentro de la estadística existe un concepto que, sin necesidad de gráficas, resulta confuso para mucha gente, el periodo de retorno, la probabilidad que se mide en años.

Caramba, yo pensaba que la probabilidad no tenía unidades, siempre la he visto como un porcentaje.

Es que no tiene unidades. En teoría, el periodo de retorno es un “tiempo medio” asociado a una probabilidad, pero en la práctica (y en la prensa) ambos conceptos se confunden, confundiendo también al lector, ya de paso, que termina pensando que algo con un periodo de retorno de 10 años ocurre siempre cada diez años, cual exacto reloj suizo.

Ah, ¿y no es así?

Pues no, por eso he decidido escribir sobre el tema. Pretendo explicar qué es el periodo de retorno sin utilizar ni una sola fórmula, ni una sola, ¿te interesa leerlo?

Pues no es que me apasione el tema, la verdad. Te doy siete minutos, ni uno más.

Algo es algo. Vamos allá. Supongamos que nos encargan el estudio de un determinado fenómeno independiente (terremoto, precipitación, lo que sea). Lo primero y principal es buscar información fiable, así que revisamos páginas y más páginas polvorientas (o bases de datos informatizadas, en el mejor de los casos) y recopilamos un montón de ocurrencias del fenómeno a lo largo de los años.

¿Es fácil conseguir esos datos?

No, ni de coña, normalmente el mayor problema es la ausencia de datos (y no digamos ya fiables), pero como se trata de un ejemplo voy a poner las cosas fáciles y suponer que tenemos datos anuales de los últimos 1.000 años (por números que no sea), y que quedan de esta forma, más o menos.

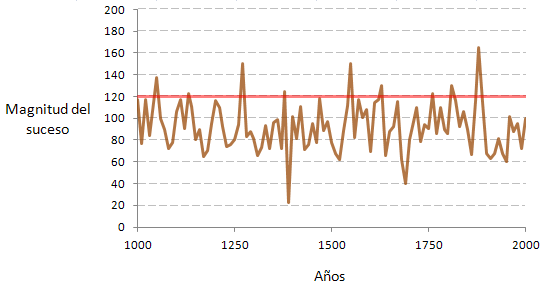
Como es lógico, el fenómeno se habrá producido con mayor o menor intensidad a lo largo del tiempo, y lo normal es que nos interese saber cuándo ha superado cierto valor máximo (terremoto de magnitud x, lluvia de determinada intensidad, etc) así que nos fijaremos en los valores que superan cierta cota (para este ejemplo, he tomado los que superan la magnitud 120).

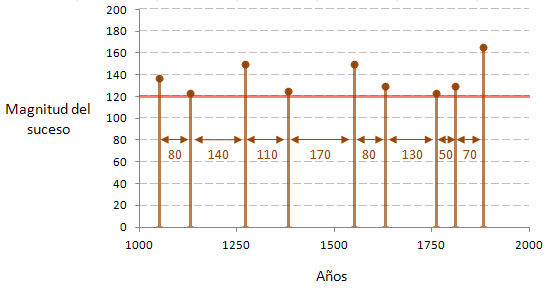
Evidentemente, estas ocurrencias máximas no son periódicas, la naturaleza es muy bonita y todo eso, pero lo que se dice exacta, no lo es mucho. En este ejemplo, el valor 120 se ha superado 9 veces en los últimos 1.000 años, en intervalos que oscilan entre 50 y 170 años.

¿Y ahora qué hacemos?

Estudiar muy bien los datos y tomar un valor lo más representativo posible de su comportamiento. Para este ejemplo simplificado supondremos que, de media, la superación del suceso se ha producido cada 100 años, repito, de media.

Ese tiempo medio entre sucesos independientes es lo que llamamos “periodo de retorno“, y nos permite cuantificar la probabilidad del evento, ya que si estamos suponiendo que el suceso se supera una vez cada 100 años, podemos suponer también que la probabilidad de dicha superación en un año cualquiera será de 1/100.

O sea, que la inversa del periodo de retorno resulta ser la probabilidad anualde superación del suceso. Si tiene un periodo de retorno de 100 años, su probabilidad anual media será de 1/100.

Vale, entendido, el periodo de retorno es el tiempo medio entre sucesos y está relacionado con la probabilidad de cada año, ¿y qué pasará al cabo de 100 años?

Me alegra que me hagas esa pregunta. Para estudiar cómo “se acumula” la probabilidad con el tiempo hay que tener en cuenta dos detalles:

1. En los sucesos independientes, la probabilidad de ocurrencia conjunta es el producto de probabilidades.
2. Como la ocurrencia sólo se producirá una vez, estudiaremos la probabilidad conjunta de los años en los que no se produce el suceso.

Eso último no lo entiendo, ¿por qué no trabajamos directamente con la probabilidad de superación, de 1/100?

Puede resultar un poco confuso, al principio, pero tiene su lógica. Queremos saber cuál es la probabilidad acumulada al cabo de 100 años… 100 años seguidos en los que no se ha superado el suceso (si lo hubiera hecho ya no serían 100 años seguidos), por tanto, a esos años les corresponde la probabilidad anual de no-superación del suceso.

Vale, ya está claro, te dejo seguir.

Muy amable, sigo entonces, que hay prisa.

Si la probabilidad de superación es del 1% (1/100), la probabilidad de no-superación será del 99% = 0,99

La probabilidad de no-superación de dos (2) años seguidos será: 0,99·0,99 = 0,99² = 0,9801 (98,01%)

Para tres (3) años seguidos será:  0,99·0,99·0,99 = 0,99³ = 0,9703 (97,03%)

Y para 100 años será:  0,99¹⁰⁰ = 0,366 (36,6%).

Es decir, que la probabilidad de no-superación del suceso en 100 años seguidos será del 36,6%.

Restando el 100% tendremos la probabilidad de superación, que será de 100% – 36,6% = 63,4%

Por tanto, pasados 100 años, la probabilidad de que se produzca un suceso con un periodo de retorno de 100 años es del 63,4%.

¡¡ Del 63,4% !!, ¿y por qué no del 100%?

Porque, desde el principio hemos dicho que el periodo de retorno de 100 años y la probabilidad anual asociada de 1/100 eran valores medios a partir de los datos disponibles, y no certezas matemáticas exactas (evidentemente, cuanto más elevada sea la probabilidad, más se acercará al periodo de retorno conforme pase el tiempo, pero seguirá siendo una probabilidad).

Entonces, cuando dicen eso de “el periodo de retorno de un terremoto gordo en España es de 100 años y el último fue en 1884, ya debería haber llegado uno gordo“… ¿no es cierto?

No, al menos no desde un punto de vista estadístico. Ese terremoto gordo podría haber llegado hace 50 años, podría producirse mañana o podría tardar todavía 80 años en llegar, y cada opción tendría su probabilidad asociada, que no tiene por qué ser exacta, además.

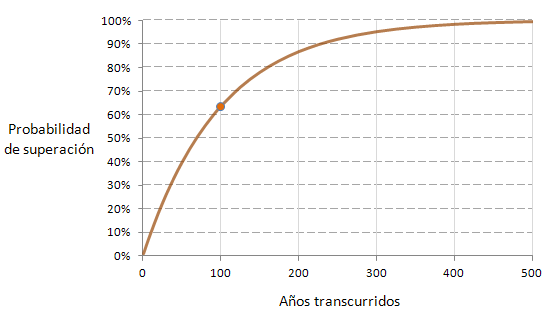
Pégale un vistazo a la gráfica y compruébalo, la marca corresponde a la probabilidad para 100 años pero la probabilidad para 200 años ni siquiera llega al 90%.

¿Y así calculáis los ingenieros? No lo veo muy fiable, que digamos.

La naturaleza no es fiable, joven padagüan, al menos no a escala humana. La fiabilidad de los cálculos depende de la fiabilidad de los datos de partida y del mayor o menor conocimiento del fenómeno. A mayor información, más podremos “afinar” las predicciones, pero sin olvidar que un fenómeno natural es imposible de predecir al 100%.

Por eso se sigue investigando y recopilando información, y por eso las teorías y normativas se van actualizando con esas observaciones y esos nuevos descubrimientos, porque trabajamos con probabilidades a partir de datos insuficientes y, lo que es peor, asumimos responsabilidades bajo esas probabilidades.

Vale, vale, no te pongas en plan víctima, ya lo he pillado… ¿qué más?

Nada más, por ahora. Me he tomado ciertas licencias y supongo que un estadístico estricto me daría un tirón de orejas (como poco), pero es el precio a pagar por no usar fórmulas, así que yo lo dejaría aquí. ¿Qué tal?, ¿ha quedado más o menos claro?

Psche, más o menos, supongo que tendré que leerlo otra vez. Lo que no entiendo es por qué las noticias sobre estos temas son siempre tan confusas.

Ya, bueno, tendrás que preguntar a los que escriben esas noticias, yo he hecho lo que he podido.

Modelo de Valoración de Activos por Arbitraje (APT)

“Modelo según el cual una cartera óptima estará constituida por aquellos valores que proporcionen un rendimiento máximo para el riesgo soportado, definido éste por su sensibilidad a los cambios económicos inesperados, tales como los cambios imprevistos en la producción industrial, en el ritmo de inflación y en la estructura temporal de los tipos de interés.”

Este modelo comienza suponiendo que la rentabilidad de cada acción depende en parte de factores o influencias macroeconómicas y en parte de sucesos que son específicos de esa empresa.

La rentabilidad viene dada por la siguiente fórmula:

Rentabilidad = a + b₁ (r_{factor 1}) + b₂ (r_{factor 2}) + b₃ (r_{factor 3}) + ... + perturbaciones

En definitiva, el APT establece que los inversionistas desean ser compensados por todos los factores que sistemáticamente afectan el rendimiento del activo. Esta compensación es la suma de los productos de la cantidad  de riesgo sistemático por cada factor, por el premio del riesgo asignado por los mercados financieros a cada uno de esos factores.

El modelo APT no establece cuáles son esos factores, algunas acciones serán más sensibles a un determinado factor que a otro.

Para una acción individual hay dos fuentes de riesgo. La primera es el riesgo que proviene de los perniciosos factores macroeconómicos que no pueden ser eliminados por la diversificación. La segunda es que el riesgo proviene de posibles sucesos que son específicos para la empresa. La diversificación hace eliminar el riesgo único, y los inversores diversificados pueden, por consiguiente, ignorarlo cuando están decidiendo si comprar o vender una acción. La prima por riesgo esperado de una acción es afectada por el  factor o riesgo macroeconómico, no viene afectado por el riesgo único.

La teoría de la valoración por arbitraje manifiesta que la prima por riesgo esperado de una acción debe depender de la prima por riesgo asociada con cada factor y la sensibilidad de la acción a cada uno de los factores ...

 Pasos para la aplicación del modelo:

Resumiremos las etapas en que se divide este modelo, para su mejor comprensión:

1.      Identificar los factores macroeconómicos que afectan a una determinada acción.

2.      Estimar la prima de riesgo de los inversores al tomar estos riesgos de los factores.

3.      Estimar la sensibilidad de cada acción a esos factores: se deberán observar los cambios ocurridos en el precio de una acción y ver cuán sensibles han sido a cada uno de los factores.

4.      Calcular las rentabilidades esperadas: se deberán aplicar los valores por prima de riesgo y las sensibilidades del factor en la fórmula de APT, para estimar la rentabilidad requerida por cada inversor.

Para concluir, hay que destacar que el APT tiene aspectos que lo hacen promisorio para determinar el rendimiento esperado de un activo financiero. No obstante, cambia los problemas del CAPM de determinar la cartera de mercado verdadera por el problema de establecer cuáles son los factores de riesgo sistemático y la medición de los factores.

El Modelo de Mercado

En el modelo de mercado, a diferencia del CAPM, la rentabilidad de la acción depende direc­tamente de la rentabilidad del mercado:

El modelo refleja la intuición práctica de todos los inversores de que el com­portamiento del mercado afecta a todas las acciones. La beta obtenida en el CAPM, en el APT y en el modelo de mercado es la misma numéricamente y su interpretación es exactamente la misma. La diferencia, desde el punto de vista de los resultados, está en el coeficiente alfa. Las fórmulas de CAPM y modelo de mercado son iguales si hacemos:

Si beta es próxima a 1, el valor del término independiente alfa debería ser cero; y también si la rentabilidad libre de riesgo es pequeña, el término independiente es insignificante.

Los coeficientes alfa y beta se calculan por regresión con datos históricos de la rentabilidad de la acción y la de un índice bursátil. Para hacer previsiones utilizamos estos pará­metros ya calculados y una estimación de la rentabilidad futura del mercado.

            

En cuanto al riesgo total, este modelo nos plantea que se puede dividir en dos componentes:   

El riesgo sistemático, o de mercado, y el no sistemático.

                  

Cuanto más grande sea la b, más volatilidad (s_s) tendrá la acción, pues reaccionará más ante los movimientos del mercado. Además del riesgo de mercado, la acción puede tener volatilidad por otras razones ajenas al mercado. Esta volatilidad es la que se puede eliminar mediante la diversificación, combinando en nuestra cartera esta acción con otras. En efecto, si en una cartera metemos muchas acciones, al final la cartera será muy similar al mercado (al índice bursátil, ya que contendrá la mayoría de las acciones del índice), y por tanto su riesgo será todo él riesgo de mer­cado. Lógicamente, si el riesgo de la cartera es el del mercado, también la rentabili­dad será la del mercado. O en otras palabras, si ponemos muchas acciones distintas y elegidas aleatoriamente en una cartera, la beta de la cartera tiende a ser uno.

Por otra parte, los movimientos de la acción provenientes del riesgo sistemático o de mercado, son explicados por R², que es el coeficiente de correlación r al cuadrado.

El R² varía mucho de una acción a otra. Para acciones de empresas grandes y estables, que tienen mucho peso en el índice, suele superar el 50 por 100. Un R² bajo se obtiene en el caso de pequeñas empresas, donde puede darse el caso de que el coeficiente beta sea alto, y aquí no podría utilizarse el modelo para hacer previsiones de rentabilidad, ya que la acción tendría un gran componente de riesgo no sistemático.

Las dificultades de orden práctico son similares que para el CAPM.

Modelos Multifactoriales

Estos modelos intentan responder a la interrogante de qué otros factores, además del mercado, afectan a la rentabilidad de una acción, cuestión que los modelos tratados con anterioridad no pueden responder.

En los modelos multifactoriales, la variable explicada o dependiente es la renta­bilidad de la acción. Las variables explicativas o independientes pueden ser, además de la rentabilidad del mercado, por ejemplo: el PER de la acción, la rentabilidad por dividendos, el nivel de endeudamiento de la empresa, el ratio valor de mercado/valor contable de la acción, los tipos de interés esperados, etc. En general, cualquier variable que intuimos puede tener influencia en la rentabilidad de la acción.

Donde:

rs            = Rentabilidad histórica de la acción o variable explicada.

C1 ... Cn = Variables explicativas (PER, endeudamiento, etc.), datos pasados.

a            = Término independiente de la regresión.

e            = Errores

b1 ... bn = Coeficientes de las variables explicativas.

Es decir, según este modelo, el precio de un activo financiero no sólo debe reflejar la prima de riesgo de mercado, sino también la prima de riesgo de factores extramercado.

En primer lugar, se debe determinar qué variables explicativas se van a utilizar y su respectivo coeficiente beta.

Para ello hacemos una regresión multivariable con datos históricos.  Así identificamos las variables que realmente han tenido influencia en la rentabilidad de la acción durante los últimos cinco años.

El paso siguiente es ver el R², que nos dice qué porcentaje de la variabilidad de la acción es explicado por las variables del modelo. Comparamos éste con el que obteníamos con el modelo de mercado (regresión rentabilidad de la acción con rentabilidad del mercado), para ver si las nuevas variables explicativas que hemos añadido al modelo aportan algo. Si la diferencia surgida es pequeña, quizá no sea de utilidad el modelo multifactorial. No así si la diferencia es grande.

Finalmente, eliminamos las variables no explicativas (las que tienen una beta no sig­nificativa) y agregamos otras posibles variables y volvemos a hacer la regresión. Paramos cuando hayamos encontrado un modelo que tenga un R² ajustado notable­mente superior al que obteníamos con el modelo de mercado.

Ahora podremos hacer una previsión de la rentabilidad de la acción usando la siguiente ecuación, pero ahora con valores esperados, es decir, poniendo los valores que esperamos en cada variable explicativa:

Con estas estimaciones obtendríamos la rentabilidad esperada de la acción, pero podemos encontrarnos con errores:

-     Que nos hayamos equivocado en nuestra estimación de las variables explicativas, es decir, que no hayamos incluido variables que sí influían en la cotización de la acción.

-    Que el modelo no funcione para el período próximo, aunque sí funcionara durante los pasados cinco años.

La evidencia empírica muestra que el poder predictivo de los modelos multifac­toriales es reducida; pero sí ha mostrado que otras variables, además de la rentabili­dad del mercado, contribuyen a explicar la rentabilidad de la acción; o en otras palabras, el modelo de mercado se puede completar.

El problema principal de este modelo es que es poco estable (lo que ha ocurrido en el pasado no es necesariamente un buen estimador de lo que pasará en el futuro); las ventajas más importantes son el ahorro de costos y la coherencia de la composición de carteras con los datos que tenemos del pasado.